Mathematical Model is a mathematical structure expressed in general or approximately, which uses visual mathematical language referring to characteristics or the dependent relationship between the numbers of some system. In the following, we take an example of setting up a function model to illustrate the application of mathematical modeling in solving practical problems.
Picture 1 Lupu Bridge
Example: The arch of Lupu Bridge can approximately be regard as a part of the parabola. On 1:11000 scale drawing of the bridge section, span AB=5cm, arch rise OC=0.9cm, line segment DE represents the length of the inside bridge arch, and DE∥AB, as shown in graph (2). On the scale drawing, regard the straight line AB as the X-axis, and parabolic axis of symmetry as the Y-axis. Plane rectangular coordinate system is established with 1 cm per unit length of the number axis. As shown in graph (3).
Graph（2）
Graph（3）
(1) Determine the function of the parabola in graph (2), and write domain of the function.
(2) If the distance OM=0.45cm between line DE and line AB, work out the actual length of Lupu inside bridge arch. (backup data: 
,and the calculation results accurate to 1m )
Solution: (1) Due to the vertex C on the Y-axis, we suppose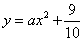 
is the function of the parabola.
Due to point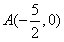 
or point 
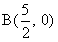on the parabola, we can get 
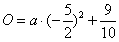, and 
.
So the analytic expression for requested function is:
(2) Because the ordinate is 1 for point D and E, we can get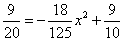 
, and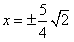 
.
Correspondingly, the coordinate of point D is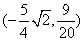 
, and the coordinate of point E is 
.
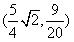We can get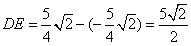 
.
So the actual length of Lupu inside bridge arch is:
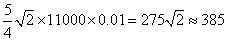m
Illustration:
The above is example of solving the problems about the bridge with knowledge of the quadratic function. We need to choose the expression of the function and set up the quadratic function model to solve such problems.
Because the parabola is axisymmetric graph, we should establish rectangular coordinate system appropriately in problems about parabolic bridges, and just work out the intersection point coordinate of the parabola, X-axis and Y-axis. Formula of parabola can be determined just according to the method in the example above.
Discussion：
How the coefficient of y＝ax2＋bx＋c influences the shape of bridge arch?
We know the image of the quadratic function is a parabola, but not all of the parabolas are the same. For example, parabolas can be different on the opening degree, on the growth speed of function value along with the increase of the independent variable, and so on. Thus, It is necessary for us to study how the coefficient of y＝ax2＋bx＋c influences the shape of bridge arch, and then decide to choose parabolic arch bridges of different shapes under different conditions.
In learning the quadratic function, we studied function y＝ax2, form of y＝ax2＋k, form of y＝a(x－h)2, and the form of y＝a(x－h)2＋k at last. We also know these functions have the same image shape and have different positions. Image of y＝ax2＋k obtained from moving up or down of image of y＝ax2, image of y＝a(x－h)2 obtained from moving right or left of image of y＝ax2, and image of y＝a(x－h)2＋k obtained from moving right or left and up or down of image of y＝ax2. So we can judge that the image of y＝ax2＋bx＋c is determined by a. In images of y＝x2 and y＝2x2, we can get that the image of y＝x2 opens larger, and images of y＝－x2 and y＝－2x2 are X-axisymmetric with images of y＝x2 and y＝2x2 respectively, so they have the same opening degree. That is to say, when |a| is large, the opening degree of image will be small.
Parabolic arch bridges of different shapes have different heights and spans. The parabola as shown in graph 4, can establish a rectangular coordinate system with the height of the river as the X-axis.
Graph 4
Suppose the parabolic expression is y＝ax2＋c(a＜0)，and the span is the length of line segment AB which represents distance between the two intersection points of the parabola y＝ax2＋c and X-axis. The height is the length of line segment OC, so C(0，c)，and (c＞0). With ax2＋c＝0，we can get x1＝－
，x2＝
, so AB＝－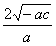
．
The above expressed the relationship between the special shape of y＝ax2＋c(a≠0) and its coefficient. The relationship between the shape of y＝ax2＋bx＋c(a≠0) in general type and a, b, c is:
y＝ax2＋bx＋c＝a(x－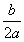
)2＋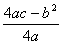
．
The height of the arch bridge is determined by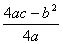 
, and the span AB is determined by AB＝
.
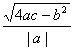The shape of the arch bridge is determined by the height and span of the bridge. Of course, for special cases we should take special treatment. That we studied is the general case, and for a specific problem the treatment should be special.
The shape of the arch bridge can be divided into circular arch bridge (through parabolic arch bridge), parabolic arch bridge (half-through parabolic arch bridge) and catenary arch bridge (deck parabolic arch bridge). This time we studied is the parabolic arch bridge. As shown in picture 5, three kinds of the arch models can be directly found that their only differences are the locations of the bridge deck. If the locations of the bridge deck are not taken into account, and under the premise that bridges have the same shape, the three kinds of conditions can be summed up in one model and discussed.
（deck parabolic arch bridge） （half-through parabolic arch bridge） （through parabolic arch bridge）
Picture 5
